=================================================================================
In machine learning, a "kernel" has a few different meanings, but the most common one refers to a mathematical function that computes the similarity between two data points in a high-dimensional space. Kernels are often used in support vector machines (SVMs) and other algorithms to enable them to work effectively with non-linear data. Here's a more detailed explanation:
Kernel Functions: In machine learning, a kernel function is a function that takes in two data points and returns a measure of their similarity. This similarity is often used to transform the data into a higher-dimensional space, making it easier to separate classes or perform other machine learning tasks. Common kernel functions include the linear kernel, polynomial kernel, radial basis function (RBF) kernel, and more. These functions allow you to implicitly map the data into a higher-dimensional space without explicitly calculating the transformations.
-
Kernel Trick: The concept of the "kernel trick" is essential to understanding the utility of kernels in machine learning. The kernel trick allows you to compute the dot product between data points in the higher-dimensional space without explicitly transforming the data, which can be computationally expensive or even impossible for very high-dimensional spaces. This makes it possible to work with high-dimensional data without actually computing the transformation explicitly.
These kernel functions, K(x,z), are used to transform data into a higher-dimensional space to make it easier to classify non-linear data. Table 4025a list the comparisons of different kernels and filters and their applications.
A two-dimensional neural network, often referred to as a 2D neural network or a 2D convolutional neural network (CNN), is a type of artificial neural network architecture specifically designed for processing and analyzing two-dimensional data, such as images and video frames. It is an extension of the traditional one-dimensional neural networks used for tasks like text and sequence processing.
In a 2D neural network, the primary building block is the convolutional layer. This layer applies filters (also called kernels) to local regions of the input data, capturing different features or patterns present in the input. The convolutional layer is particularly well-suited for tasks where the spatial arrangement of data is important, such as image recognition, object detection, and image segmentation.
Kernels are not limited to just Support Vector Machines (SVMs). They are a general concept used in various machine learning and mathematical techniques to transform data into a higher-dimensional space, which can make it easier to find patterns and relationships in the data.
Table 4025a. Kernels and filters and their applications.
| Kernel |
Formula |
Pros (Advantages) |
Cons (Disadvantages) |
Applications |
| Linear Kernel |
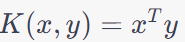
 |
Simple and computationally efficient. |
Works well only for linearly separable data. |
Text classification (e.g., spam detection), Sentiment analysis, Basic image classification tasks. This is the most widely used kernel. |
| Polynomial Kernel |
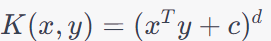
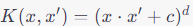 |
Can capture polynomial relationships in the data. |
Sensitive to the choice of the degree parameter. Can lead to overfitting. |
Image classification, especially when dealing with non-linear features,
Object recognition in computer vision,
Speech recognition with non-linear features. |
| Radial Basis Function (RBF) Kernel (Gaussian Kernel) |
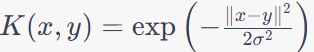
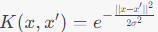 |
Versatile and can capture complex, non-linear decision boundaries. |
Sensitive to the choice of the hyperparameter "γ", which affects the shape of the decision boundary. |
Handwritten digit recognition,
Image segmentation,
Bioinformatics for protein structure prediction. The Laplacian kernel is closely related to the RBF kernel, and they share some similarities. This is the secondly widely used kernel. |
| Sigmoid Kernel |
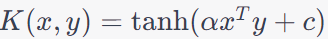 |
Can be used for data with sigmoid-like patterns. |
Sensitive to the choice of hyperparameters. Not as widely used as other kernels. |
Financial time series analysis,
Anomaly detection in network traffic,
Speech emotion recognition. |
| Laplacian Kernel |
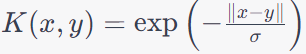 |
Similar to the RBF kernel, but with a different shape. |
Requires tuning of the hyperparameter. |
Image denoising and restoration,
Data clustering,
Hyperspectral image analysis. The Laplacian kernel is closely related to the RBF kernel, and they share some similarities. |
| Bessel Function Kernel |
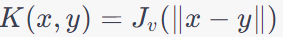 |
Rarely used in practice, but it can handle periodic data. |
Less common and may require careful parameter tuning. |
Sonar signal processing, Seismic data analysis, Acoustic signal processing. Bessel Function kernels are not standard kernels in ML and are less commonly used than kernels like linear, polynomial, RBF, or sigmoid kernels. |
| Spline Kernel |
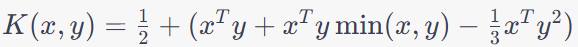 |
Useful for smoothing and interpolating data. |
More commonly used in regression tasks rather than classification. |
Function approximation and regression, Interpolation in computer graphics, Predictive modeling in environmental science. |
| Inverse Multiquadric Kernel |
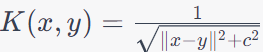 |
Can capture both short and long-range dependencies in the data. |
Requires hyperparameter tuning. |
Geostatistics for spatial data analysis, Geophysical signal processing, Modeling biological systems. |
| Chi-Square Kernel |
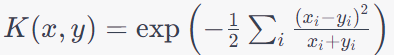
|
Suitable for histograms and discrete data. |
Less common for standard classification tasks, and its utility depends on the nature of the data. |
Image retrieval using histograms, Document retrieval and text mining, Bioinformatics for sequence alignment. |
| Histogram Intersection Kernel |
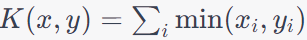 |
Well-suited for histogram data and similarity-based tasks. |
Not widely used in standard SVM classification. |
Object recognition in computer vision, Document image retrieval, Information retrieval for multimedia data. |
Table 4025b. Applications of kernels.
| Algorith |
Details |
| Kernel Methods |
Besides SVMs, other kernel methods like Kernel Ridge Regression, Kernel Principal Component Analysis (Kernel PCA), and Kernel Canonical Correlation Analysis (KCCA) use kernels to perform nonlinear transformations and feature mappings. |
| Kernelized k-Means |
In kernelized k-Means clustering, a kernel function is used to implicitly map data points into a higher-dimensional feature space, allowing non-linear separation of clusters. |
| Gaussian Processes |
Gaussian processes can use kernels to define the covariance structure of functions, making them useful for regression and probabilistic modeling. |
| Kernel Density Estimation |
Kernels are used in kernel density estimation to estimate the probability density function of a random variable. |
| Spectral Clustering |
Spectral clustering can be kernelized, allowing it to work in non-linear feature spaces. |
| Radial Basis Function Networks (RBF Networks) |
Radial basis function networks use radial basis function kernels to model complex relationships in data. |
| Image Processing |
Kernels are commonly used in image processing for tasks like image smoothing, edge detection, and texture analysis. Convolutional neural networks (CNNs) can also be viewed as using convolutional kernels for feature extraction. |
| Natural Language Processing |
In NLP, kernels can be used in text classification tasks, sentiment analysis, and other applications to capture non-linear relationships in text data. |
| Computational Biology |
Kernels are used in various bioinformatics applications, such as protein structure prediction and gene function prediction. |
| Anomaly Detection |
Kernel methods can be applied to detect anomalies or outliers in data by modeling complex patterns and deviations from expected behavior. |
| Graph Kernels |
Graph kernels are used in graph-based machine learning tasks, such as graph classification and clustering. |
| Time Series Analysis |
Kernels can be applied to time series data for tasks like similarity measurement and forecasting. |
Table 4025c. Feature mapping for 3D input vector X.
| Feature mapping |
Definition |
Feature mapping for 3D input vector X |
Computational complexity |
| Linear Features |
These are just the original features themselves |
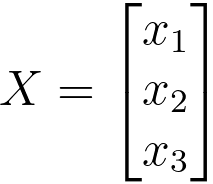 |
O(n): The linear feature mapping involves simply copying the original features, so the computational complexity is linear in the number of input features. |
| Quadratic Features |
These are the square of each feature |
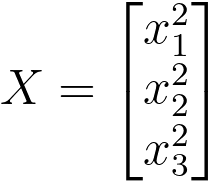 |
O(n2): The quadratic feature mapping involves calculating the square of each original feature. For each feature in the original input, we need to perform a multiplication operation. Since there are n input features, this results in a quadratic computational complexity. |
| Interaction Features |
These are pairwise products of the original features |
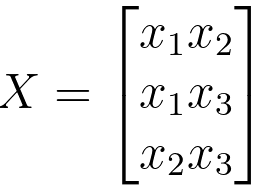 |
O(n2): The interaction feature mapping computes pairwise products of the original features, resulting in n(n-1)/2 pairwise products. |
| Polynomial Features |
The polynomial feature mapping includes the following types of features for the three-dimensional input vector X:
1. Constant Term: The first feature is a constant term, which is always set to 1. This term allows the model to capture the bias or offset in the data.
2. Linear Features: The next three features are linear terms. These features are the original features themselves, scaled by the square root of 2. In the feature mapping, they are represented as:
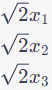
3. Quadratic Features: The following three features are quadratic terms. These features are the squares of the original features, and they are represented as:
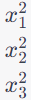
4. Interaction Features: The final three features are interaction terms. These features represent pairwise products of the original features, each scaled by the square root of 2. They are represented as:
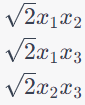
This feature mapping captures a variety of polynomial and interaction terms, allowing a machine learning model to capture non-linear relationships in the data when used as a kernel function in algorithms like Support Vector Machines (SVMs) with a polynomial kernel. |
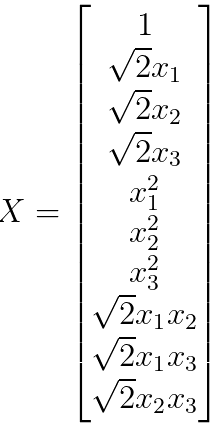 |
O(1) for Constant Term; O(n) for Linear Features; O(n2) for Quadratic Features; O(n2) for Interaction Features. Then, total is O(1) + O(n) + O(n2) + O(n2) |
Assuming kernel features for a three-dimensional input vector X:
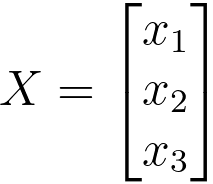 ---------------------- [4025a] ---------------------- [4025a]
Here, X ⊂ℝn (n = 3).
Let's choose a feature mapping as,
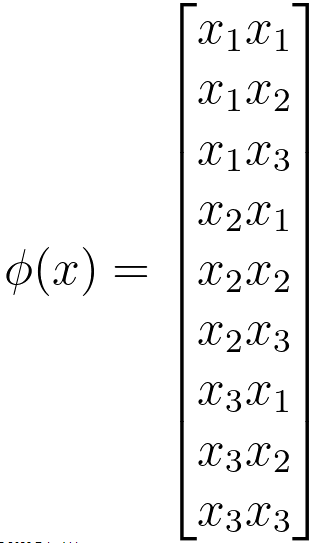 ---------------------- [4025b] ---------------------- [4025b]
Here, Φ ⊂ℝn^2 (n = 3 and n2 = 9), then Φ is 9 dimensional.
Assuming, we also have,
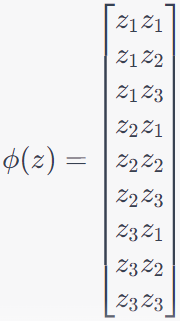 ---------------------- [4025c] ---------------------- [4025c]
Then, we can have,
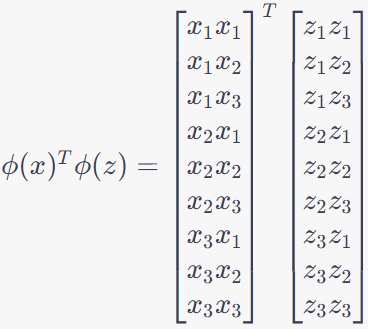 ---------------------- [4025d] ---------------------- [4025d]
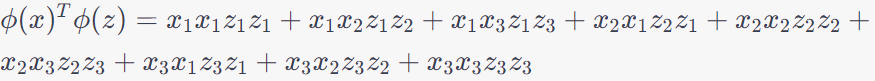 ---------------------- [4025e] ---------------------- [4025e]
On the other hand, we have,
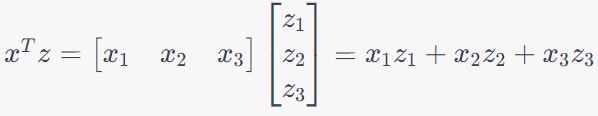 ---------------------- [4025f] ---------------------- [4025f]
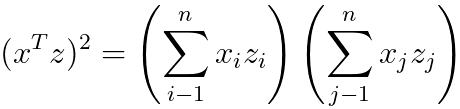 ---------------------- [4025fa] ---------------------- [4025fa]
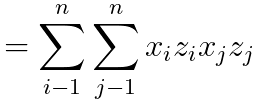 ---------------------- [4025g] ---------------------- [4025g]
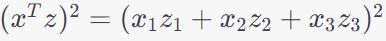 ---------------------- [4025ga] ---------------------- [4025ga]
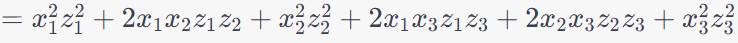 ---------------------- [4025h] ---------------------- [4025h]
Then, we have,
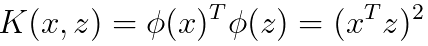 ---------------------- [4025i] ---------------------- [4025i]
Since x and z are n-D (n dimensional), then (xTz)2 is n4 time of computing time, which the φ(x)Tφ(z) is n2 time of computing time.
If we add a constant into Equation 4025i, then we have,
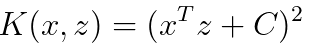 ---------------------- [4025j] ---------------------- [4025j]
Then, we can assuming,
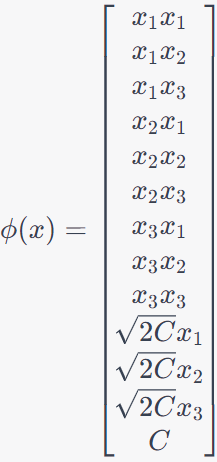 ---------------------- [4025k] ---------------------- [4025k]
If we have,
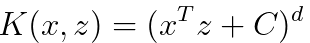 ---------------------- [4025l] ---------------------- [4025l]
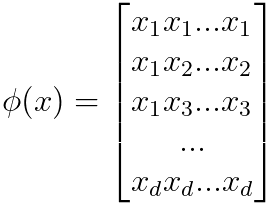 ---------------------- [4025m] ---------------------- [4025m]
In this feature mapping, we are capturing all possible pairwise products of the original features. This transformation creates a new set of features that represent the interactions between the original features in a three-dimensional input space. This feature mapping can be used in various machine learning algorithms, such as kernel methods, to work with non-linear data and capture complex relationships between features. It's a valid choice for creating a feature representation of our data. The feature mappings like the one shown in Equation 4025b can be applied in various machine learning algorithms to capture non-linear relationships and interactions between features. Table 4025c lists some applications of such feature mappings.
Table 4025c. Some applications of such feature mappings shown in Equation 4025b.
| Algorithm |
Details |
| Support Vector Machines (SVM) |
SVMs are particularly suitable for handling non-linear data when combined with appropriate kernel functions. The chosen feature mapping can be used as a kernel function in an SVM to classify data in a higher-dimensional space, allowing SVMs to capture complex patterns and decision boundaries. |
| Kernel Methods |
Kernel methods, in general, can benefit from such feature mappings. By applying this feature mapping to input data, we can use it in kernel-based algorithms like the Kernelized Support Vector Machine (SVM), Kernelized Ridge Regression, or Kernelized Principal Component Analysis (PCA) to capture complex relationships between features. |
| Naive Bayes |
Naive Bayes is a probabilistic classification algorithm. While it's based on the assumption of feature independence, we can still use feature mappings to capture complex dependencies between features. However, using such feature mappings may violate the "naive" independence assumption, so it's important to assess the impact on performance carefully. |
| Kernel Ridge Regression |
Kernel Ridge Regression is a regression technique that can benefit from non-linear feature mappings. By applying the chosen feature mapping, we can capture non-linear relationships between input variables, which can improve the regression model's performance. |
| Principal Component Analysis (PCA) |
PCA can be used with non-linear feature mappings, allowing you to perform dimensionality reduction in a space that captures non-linear relationships between features. |
| Clustering Algorithms |
Feature mappings can be used in clustering algorithms like Kernel K-Means to discover non-linear clusters in data. |
| Image Processing |
In image processing, feature mappings can be applied to extract non-linear features for tasks like object recognition, texture analysis, or image segmentation. |
| Natural Language Processing (NLP) |
In NLP, feature mappings can be used to create non-linear features for text data, which can improve the performance of text classification and sentiment analysis tasks. |
| Chemoinformatics |
Feature mappings are commonly used to extract relevant features for chemical compound data to predict properties, such as solubility, toxicity, or bioactivity. |
The kernel function K(x, z) measures the similarity between data points x and z in a feature space. If x and z are similar, K(x, z) (= φ(x)Tφ(z) ) will be larger, indicating a higher similarity. The idea is that the dot product of the feature vectors φ(x) and φ(z) is larger when x and z are more similar in the feature space. Conversely, when x and z are dissimilar, φ(x)ᵀφ(z) will be smaller, suggesting a lower similarity between the two data points.
A kernel function, in machine learning and kernel methods, is a mathematical function that computes the similarity or inner product between data points in a higher-dimensional feature space without explicitly mapping the data points into that space. Kernel functions are a key component of kernel methods, such as Support Vector Machines (SVMs) and kernelized versions of various algorithms, which allow these algorithms to perform nonlinear classification and regression tasks by implicitly working in a higher-dimensional feature space.
If K is a valid kernel function, then we have,
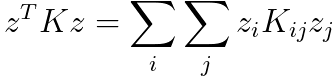 ----------------------------------- [4025o] ----------------------------------- [4025o]
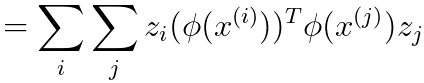 ----------------------------------- [4025p] ----------------------------------- [4025p]
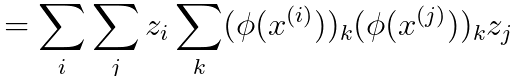 ----------------------------------- [4025q] ----------------------------------- [4025q]
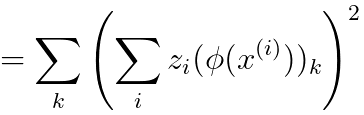 ----------------------------------- [4025r] ----------------------------------- [4025r]
Equation 4025r proves the kernel function is typically positive. In fact, to be a valid kernel function, a function K(x, z) must satisfy two essential conditions known as Mercer's conditions:
-
Symmetry: The kernel function must be symmetric, meaning K(x, z) = K(z, x) for all pairs of data points x and z. This symmetry property ensures that the order of the data points does not affect the kernel's value.
-
Positive Semidefiniteness: For any set of data points {x₁, x₂, ..., x_n}, the kernel matrix (also known as the Gram matrix), which is defined as a matrix with K(xi, xj) as its elements, must be positive semidefinite. In other words, for any vector c = [c₁, c₂, ..., c_n], the following inequality must hold:
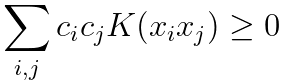 ----------------------------------- [4025n] ----------------------------------- [4025n]
If a function satisfies these two conditions, it is considered a valid kernel function, and it can be used in kernel methods to implicitly compute the inner products in a higher-dimensional feature space. The fact, which is typically positive semi-definite, is a fundamental property that kernel functions must satisfy to be valid in the context of kernel methods, such as Support Vector Machines (SVM) and kernelized regression. A positive semi-definite kernel function is a crucial requirement because it ensures that the corresponding kernel matrix (Gram matrix) formed by applying the kernel function to pairs of data points is positive semi-definite as well. In the context of SVMs, this property is essential for the algorithm to work correctly and for the resulting decision boundaries to be well-behaved.
The kernel matrix is a square matrix used in the context of kernel methods, such as SVMs and kernelized versions of various algorithms. It represents the pairwise inner products or similarities between a set of data points in a higher-dimensional feature space, without explicitly mapping the data into that space. Given a set of data points {x₁, x₂, ..., x_n}, the kernel matrix K is defined such that its elements K(xᵢ, xⱼ) represent the similarity or inner product between data points xᵢ and xⱼ in the feature space. In other words, K(xᵢ, xⱼ) equals the value of the kernel function applied to xᵢ and xⱼ, i.e., K(xᵢ, xⱼ) = φ(xᵢ)ᵀφ(xⱼ), where φ(·) is the feature mapping function that implicitly maps the data into the higher-dimensional feature space. The kernel matrix is typically used in kernel methods for various purposes, including:
-
Training SVMs: In SVMs, the kernel matrix is used to determine the support vectors and to find the optimal hyperplane that separates different classes of data points in the feature space.
-
Kernel Principal Component Analysis (KPCA): KPCA is a kernelized version of Principal Component Analysis (PCA), and it uses the kernel matrix to compute principal components in the feature space.
-
Kernelized Ridge Regression: The kernel matrix is used to regularize the regression problem, allowing for nonlinear regression tasks.
-
Clustering: The kernel matrix can be used in spectral clustering algorithms to partition data points based on their pairwise similarities.
|
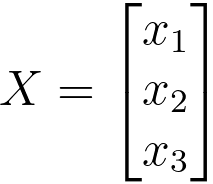
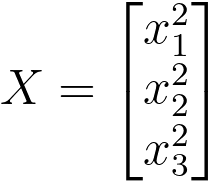
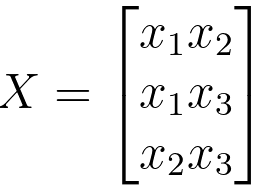
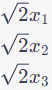
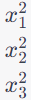
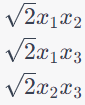
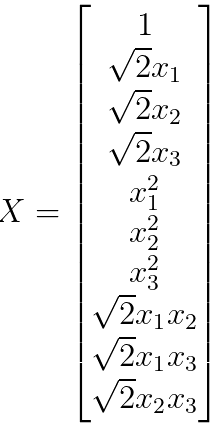
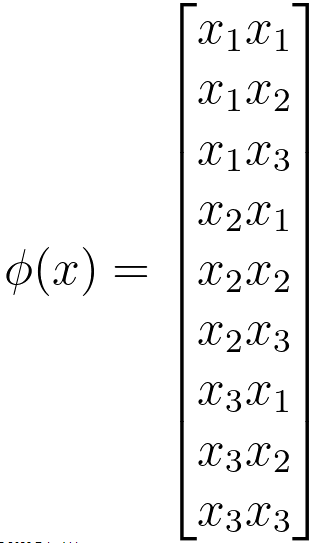 ---------------------- [4025b]
---------------------- [4025b]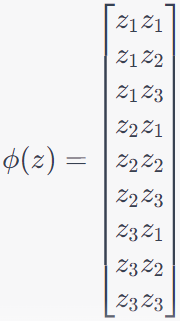 ---------------------- [4025c]
---------------------- [4025c]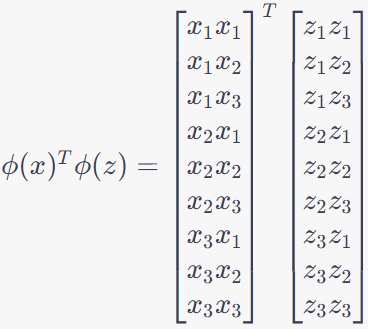 ---------------------- [4025d]
---------------------- [4025d]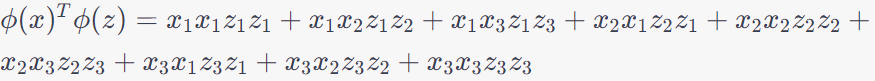 ---------------------- [4025e]
---------------------- [4025e]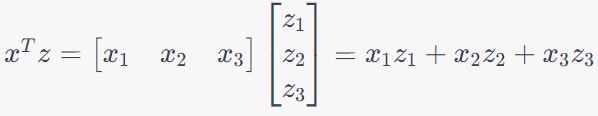 ---------------------- [4025f]
---------------------- [4025f]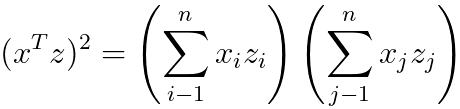 ---------------------- [4025fa]
---------------------- [4025fa]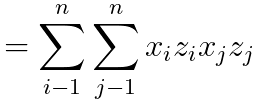 ---------------------- [4025g]
---------------------- [4025g]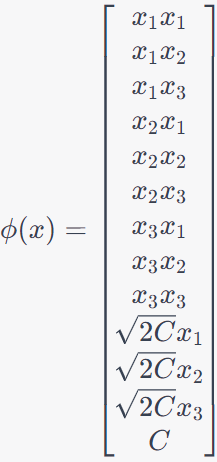 ---------------------- [4025k]
---------------------- [4025k]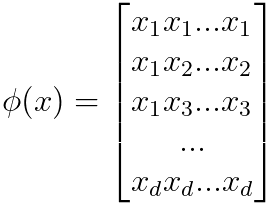 ---------------------- [4025m]
---------------------- [4025m]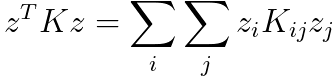 ----------------------------------- [4025o]
----------------------------------- [4025o] 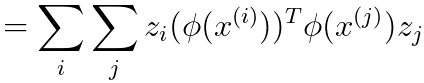 ----------------------------------- [4025p]
----------------------------------- [4025p] 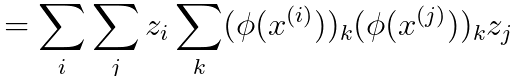 ----------------------------------- [4025q]
----------------------------------- [4025q] 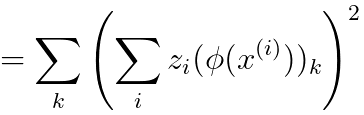 ----------------------------------- [4025r]
----------------------------------- [4025r] 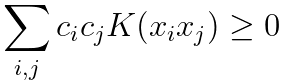 ----------------------------------- [4025n]
----------------------------------- [4025n]