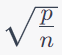=================================================================================

An infinite hypothesis class is a concept often encountered in machine learning and statistics. It refers to a set of potential models or hypotheses that can be used to represent data or make predictions, and this set is infinite in size. In contrast, a "finite hypothesis class" would be a limited set of models or hypotheses to choose from.

There are a few key points to know about infinite hypothesis classes:

1. Flexibility: Infinite hypothesis classes offer more flexibility in modeling complex relationships in data because they include an unlimited number of potential models. This allows them to potentially capture intricate patterns and structures that finite classes might miss.

2. Challenges: Dealing with infinite hypothesis classes can be computationally challenging. Searching for the best model or hypothesis within such a class may require advanced optimization techniques or approximation methods.

3. Regularization: To prevent overfitting (fitting the training data too closely and performing poorly on new data), it's often necessary to use regularization techniques when working with infinite hypothesis classes. Regularization helps constrain the models and prevent them from becoming overly complex.
4. Examples: Some examples of infinite hypothesis classes in machine learning include:

   • Linear Regression with Polynomial Features: In polynomial regression, you can include an infinite number of polynomial features (e.g., x^2, x^3, x^4, ...) to fit nonlinear data patterns.

   • Neural Networks with Infinite Hidden Units: In deep learning, neural networks with infinitely many hidden units in a layer can represent complex functions.

   • Kernel Methods: Support Vector Machines and Kernel Ridge Regression use kernel functions that can map data into higher-dimensional spaces, potentially leading to infinite-dimensional hypothesis classes.

   • Gaussian Processes: Gaussian processes are a non-parametric method that can represent a wide range of functions and are considered to have an infinite hypothesis class.

In practice, dealing with infinite hypothesis classes often involves introducing additional assumptions, regularization, or priors to make the learning problem tractable and avoid overfitting. These techniques help strike a balance between model complexity and generalization to new, unseen data.

Bounding the performance of models in an infinite hypothesis class is a complex problem, and it often depends on the specific context, assumptions, and learning framework. Consider the setting of Linear Regression:

In linear regression, you have a model like this:

          ------------------------------- [3936a]

Where:

• y is the target variable.
• β_i​ are the coefficients of the features x_i.
• p is the number of features.
• ϵ is the random error.

You want to estimate the coefficients β_i​ based on a training dataset of size n.

Potential bounds are:

i)

This is sometimes used to express the trade-off between model complexity (determined by p) and the amount of data (determined by n). When is large, you have a situation where you have more features than data points, which can lead to overfitting.

Here's how this bound works::

• If is large, it implies that the model has more parameters (features) relative to the amount of data available. In such cases, the model might fit the training data very closely but generalize poorly to new, unseen data.
• If is small, it implies that there are more data points relative to the number of features. This often leads to better generalization as the model doesn't have too many parameters to fit the training data noise.

ii) Rademacher Complexity:

Rademacher complexity measures the ability of a class of functions to fit random noise. It's often used in statistical learning theory to bound the generalization error. For a hypothesis class F, Rademacher complexity is defined as the expected value of the supremum over the randomness of the training dataset.

iii) VC Dimension:

The Vapnik-Chervonenkis (VC) dimension is a combinatorial measure of the capacity of a hypothesis class to shatter data points. If the VC dimension is d, it implies that the class can fit any set of � d data points. This dimension can be used to bound the sample complexity.

iv) PAC Learning Bounds:

In the Probably Approximately Correct (PAC) learning framework, bounds are derived for the number of samples needed to ensure that a learning algorithm produces a good hypothesis with high probability.

v) Regularization Terms:

In practical machine learning, regularization terms (e.g., L1, L2 regularization) are added to the loss function to bound the complexity of the learned model.

These bounds are often problem-specific and are used to guide the choice of model complexity, regularization, and sample size based on the specific characteristics of the data and the learning problem.

Assuming H is parameterized by Θ ∈ℝ^p then,

          H = {h_θθ: ∈≤ℝ^p} -------------------------- [3936b]

Consider and L((x,y), θ) = L(h_θ(x), y)

Assuming,

          0 ≤ L((x,y), θ) ≤ 1 for every x, y, θ

         L((x,y), θ) is k-Lipschitz in θ for every x, y.

Then, we have theorem, that is, for any θ and θ', the absolute difference of the loss functions can be bounded by K times the L2 norm of the difference between θ and θ':

          ||L((x,y), θ) - L((x,y), θ')| ≤ K||θ||₂ -------------------------- [3936c]

The Lipschitz condition is often desirable in mathematical optimization, machine learning, and other areas for several reasons:

1. Stability: A k-Lipschitz function is stable in the sense that small changes in its input parameters result in small changes in its output. This property can be valuable in situations where stability and robustness are essential.

2. Convergence in Optimization: In optimization problems, Lipschitz continuity can ensure convergence of optimization algorithms. Algorithms like gradient descent converge more reliably and predictably when dealing with Lipschitz continuous functions.

3. Generalization in Machine Learning: In machine learning, a k-Lipschitz continuous loss function can aid in better generalization. It helps control the complexity of a model and prevents it from fitting the noise in the data too closely, which can lead to overfitting.

4. Theoretical Analysis: Lipschitz continuity provides bounds and guarantees that make it easier to analyze and reason about functions mathematically.

However, whether a specific k value (Lipschitz constant) is considered "very good" or "reasonable" depends on your problem's requirements. Smaller values of k generally imply greater stability and more predictable behavior, but they might also indicate slower convergence or overly conservative generalization. Larger values of k might allow faster convergence but can result in less stable or less robust functions.

It's essential to choose a Lipschitz constant (k) that strikes a balance between your optimization or learning objectives and the constraints and stability requirements of your problem. In many cases, the choice of k involves trade-offs and often depends on empirical experimentation to find an appropriate value that works well for the specific task at hand.

============================================